数学复数是数学领域中一个充满奥秘的概念，它不仅在代数方程的解中起着重要的作用，还在电路分析、信号处理等实际应用中发挥着重要作用。本文将带领读者深入探索数学复数的知识点，了解其基本概念、性质和运算规律，揭开复数的神秘面纱。

一：什么是复数（基本概念）

复数是由实数和虚数构成的一种数，可以表示为a+bi的形式，其中a是实部，b是虚部，i是虚数单位。复数的实部和虚部可以是任意实数，虚数单位i满足i^2=-1。

二：复数的图像表示（坐标平面上的位置）

复数可以用平面直角坐标系来表示，实部对应横坐标轴，虚部对应纵坐标轴。在坐标平面上，复数对应一个点，称为复平面上的复数点。

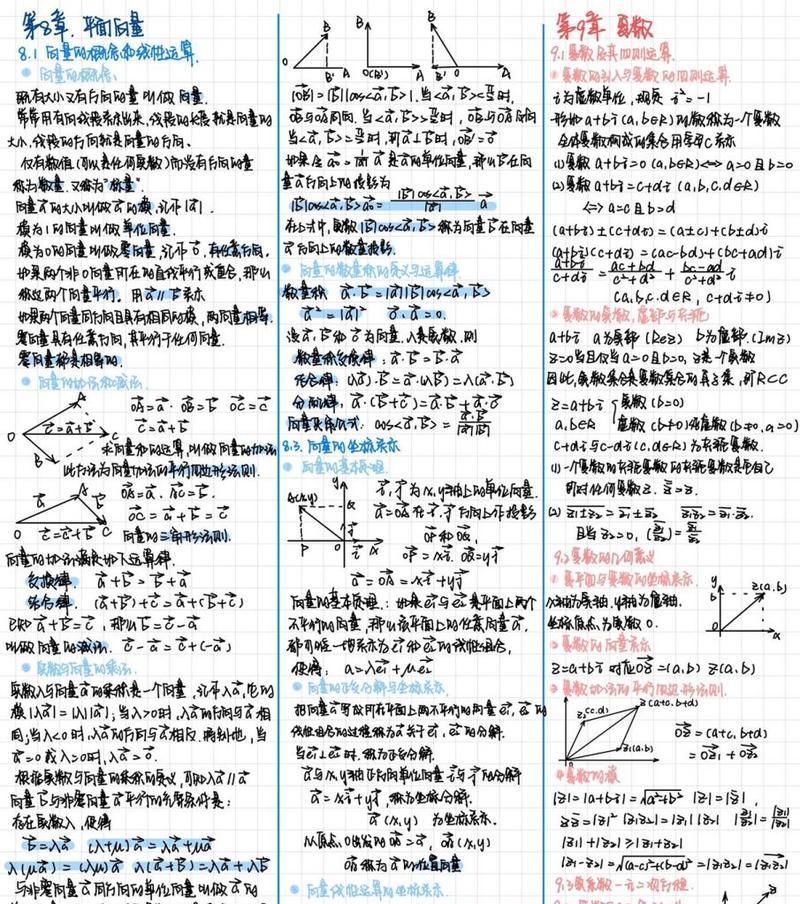
三：复数的共轭（复数的重要性质之一）

复数的共轭表示将复数的虚部取负，即a-bi。共轭具有保持实部不变而改变虚部符号的作用，这在计算复数的乘法和除法时经常用到。

四：复数的加法和减法运算（运算规律）

复数的加法和减法运算是分别对应实部和虚部进行运算，即将两个复数的实部相加（或相减），虚部相加（或相减），得到新的复数。

五：复数的乘法运算（运算规律）

复数的乘法运算是通过对应实部和虚部进行运算，根据乘法公式展开并化简，得到新的复数。乘法的结果可以看作是平移、旋转或伸缩原复数。

六：复数的除法运算（运算规律）

复数的除法运算是通过乘以分母的共轭来消去分母中的虚部，然后进行简化运算，得到新的复数。除法运算可以看作是平移、旋转或伸缩原复数。

七：复数的绝对值与参数（重要性质之一）

复数的绝对值表示复平面上从原点到该复数点的距离，参数表示该复数与实轴正半轴之间的夹角。复数的绝对值和参数可以通过实部和虚部的运算推导而得。

八：欧拉公式与复指数函数（重要性质之一）

欧拉公式是数学中的重要公式，将复指数函数与三角函数和指数函数建立了联系。欧拉公式展示了复数的指数形式和三角形式之间的关系，为解决复数问题提供了便利。

九：复数的幂运算（重要性质之一）

复数的幂运算可以通过将复数转化为指数形式，然后利用指数运算规律进行计算。复数的幂运算可以用于求解方程、计算序列等问题。

十：复数的根运算（重要性质之一）

复数的根运算是求解复数方程的重要方法，通过将复数转化为指数形式，然后利用根的运算规律进行计算。复数的根运算在代数方程的解中有广泛应用。

十一：复数在电路分析中的应用

复数在电路分析中起着重要作用，可以用来描述电路中的电流和电压关系。复数的使用简化了电路分析过程，并提供了更多解决电路问题的方法。

十二：复数在信号处理中的应用

复数在信号处理中也有广泛应用，可以用来分析和处理信号的频谱、相位和振幅等特性。复数的运算规律和性质为信号处理提供了强大的工具。

十三：复数与几何的联系

复数与几何之间存在着紧密的联系，可以用复数来描述平面上的点、直线和图形等几何概念。复数的运算规律和性质为几何问题提供了新的视角和解决方法。

十四：复数的历史背景与发展

复数的概念最早可以追溯到16世纪，但在历史上遭到了质疑和争议。随着数学的发展，复数逐渐被接受并成为重要的数学工具，推动了代数学和解析几何学的发展。

十五：复数的应用前景与

复数作为一种重要的数学工具，广泛应用于代数方程、电路分析、信号处理、几何等多个领域。对复数的深入理解有助于提高数学思维能力和解决实际问题的能力。通过本文的探索，我们希望读者能够对数学复数有更深刻的认识，并能将其灵活运用于实际应用中。

数学复数作为一种充满奥秘的数学概念，具有丰富的性质和应用。通过对复数的基本概念、运算规律和性质的探索，我们可以揭开复数的神秘面纱，了解其在代数方程、电路分析、信号处理和几何等领域的重要作用。希望本文对读者理解和应用数学复数有所帮助，并激发更多对数学的探索和兴趣。